算数の順序問題を考えるシリーズの第3回は、前回の考え方を掛け算にも応用し、四則演算に順序があったりなかったりする数学の世界を定義します。
そして、算数教科書にある掛け算・割り算の文章題の分類や数学との対応を取ります。
すると、「足し算や掛け算に順序がある」とする場合の、スッキリしない点が見えてきます。
はじめに
前回から間が空いてしまいましたが、足し算の順序問題をイジる考えるシリーズの第3回です。
振り返り
軽く前回までを振り返ってみましょう。
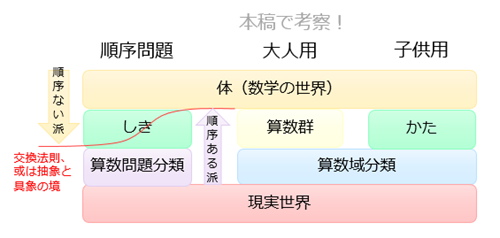
上の図が、私のイメージ図です。
一番左の建物が、私が思っているところの「算数の順序問題」です。
まず、教科書の文章問題の分類を、便宜上「算数問題分類」と名付けています。問題はその上の「しき」の階です。
「しき」が教科書の問題分類の延長だとする「順序ある派」と、「しき」は体(数学の世界)の数式と同一だとする「順序ない派」が、この階の領土の取り合いをしています。(中庸派、学年で切り替え派、どうでもいい派もいるかもしれませんね。)
一つの用語の解釈が異なってしまうのは論争の元ですので、「しき」の代わりに、順序がある数学の世界である「算数群」を定義します。(「群」と言っていますが、正確には数学の群ではありません。)私の独自の定義ですので、異なった解釈は認めません。
そして「算数問題分類」の代わりに、MECEである「算数域分類」を定義します。これも私独自の定義(ry。
これらが、真ん中の建物です。
とはいえ、「そんな独自の世界を定義しても、意味ないじゃん!」というご意見があることは、想像するに難くありません。そこで、「しき」の代わりになるものを「かた」と名付け、順序が違うだけで子供が×を付けられて悲しい思いをしたり、数学嫌いになったりしないように考えてみます。図の右側の建物です。(これは次回。)
今回のお題
前回は足し算と引き算についての、算数群、算数域分類、および算数問題分類と体との対応をとりました。
今回は前回と同様に、掛け算と割り算における算数群、算数域分類、および算数問題分類と体との対応を考えます。
算数問題分類
では、教科書における掛け算と割り算の問題の分類から見てみましょう。
本章での用語や対応する問題例は、新興出版社啓林館のサイトの「算数用語集」を参考にさせて頂きました。(用語の参照のみで、啓林館さんが順序を主張しているわけではありませんのでご了承ください。)
掛け算問題の分類
掛け算の問題には、以下のような種類があります。
| 説明 | 問題例 | |
|---|---|---|
| 同数累加 | 同じ数を何回も加えること | お皿1枚には、リンゴ4個が乗っています。お皿が3枚あるき、リンゴは何個ですか。 |
| 倍概念 | ある数量は、もう一方の数量の何倍か、という概念 | 電車1台は6mです。2台分の長さは何mですか。 |
| 長方形の求積 | 長方形、正方形の面積を求めること | 縦3cm、横4cmの長方形の面積は何cm2ですか。 |
式に書く項に順序があるとされる場合では、同数累加の「一つ分の数」を先に書き、「いくつ分」かを後に書くことになります。問題例の場合の「しき」においてはは、「4×3」は○、「3×4」は×です。
倍概念の順序はよくわかりません(ちょっと検索しましたがどうでもよくなった…)。
おそらく「何倍」を後に書くのではないでしょうか。その方が同数累加との対応が付くような気がします。(一皿のリンゴが基準の数、何倍かがお皿の数と考えれば…。)
長方形の面積は、さすがに順序はないでしょうね。
割り算問題の分類
割り算の問題には、以下のような種類があります。
| 説明 | 問題例 | |
|---|---|---|
| 等分除 | 全体を、決まった組数に同じ分量ずつ分ける場合、いくつずつになるか | 6個のクッキーを3人に分けると、一人分は何個ですか。 |
| 包含除 | 全体を、ある分量ずつに分けると、何組に分けられるか | 6個のクッキーを2個ずつ分けると、何人に分けられますか。 |
| 何倍を求める | ある数量が、基準となる数量の何倍であるかを求めること | 青い棒は2mです。赤い棒は4mです。赤い棒は青い棒の何倍ですか。 |
| もとにする数を求める | 不明なもとの数量を、何倍かにした数量があるときに、もとの数量を求めること | 4mの赤い棒は、青い棒の2倍です。青い棒は何mですか。 |
等分除と包分除が同数累加の逆演算、「何倍を求める」「もとにする数を求める」が、倍概念の逆演算です。長方形の求積に対しても逆演算が定義できそうです。
算数問題分類のまとめ
以上、掛け算と割り算の算数問題分類でした。
足し算・引き算のときと比べると、逆演算の対応ができておりキレイですね。「時間の概念が云々」のような気持ち悪さもありません。
算数域分類(独自)の定義が楽そうです。
算数群
次に、掛け算にも順序がある数学の世界を定義していきます。
算数群での演算
詳細は前回と同様ですので割愛します。
前回のように、可換と非可換の語の意味だけを以下のように上書きします。
- 可換:交換法則が成り立ち、尚且つ左右の項を入れ替えてもよいこと。
- 非可換:交換法則が成り立とうがどうであろうが、左右の項の入れ替え禁止!
そして、演算と演算子を以下のように定義します。
- 演算*:可換な乗算。演算子は”*”。
- 演算&:非可換な乗算。演算子は”&”。
すると、逆演算は以下の3つになります。
- 演算!*:可換な演算*の逆演算
- 演算!&s:非可換な演算&の、元の演算の左項を得る逆演算
- 演算!&o:非可換な演算&の、元の演算の右項を得る逆演算
以上、算数群における乗算と除算5つを定義しました。
算数域分類
算数問題分類を参考にMECEな分類を考え、算数域分類として定義します。
| 算数域分類 | 算数群の式 | 説明 |
|---|---|---|
| 求積 | S * O = P | 一部の数と、もう一部の数を掛けて、積(面積)を求めること。 S:Subject、O:Object、P:Product |
| 求倍果 | B & T = R | 大小2つの数量があり、元になる数と、何倍にするかがわかっていて、それらから結果の数量を求めること B:Base、T:Time、R:Result |
| 求項 | P !* O = S P !* S = O |
積(長方形の面積)と、一つの項(一辺の長さ)がわかっているときに、もう一つの項を得ること。 求積の逆関数。 S:Subject、O:Object、P:Product |
| 求倍数 | R !&o B = T | 2つの数量が存在し,結果の数が元の数の何倍かを得ること。 求倍増の右項を得る逆演算。 B:Base、T:Time、R:Result |
| 求基数 | R !&s T = B | 結果の数と、元の数を何倍したかがわかっていて、元の数を得ること。 求倍増の左項を得る逆演算。 B:Base、T:Time、R:Result |
「倍概念も最初のうちは同数累加と同じ考え方だろう」ということで、その両方を一緒にして「求倍果」としました。
算数問題分類、体との対応
以上、算数群と算数域分類を定義しました。
これらと、算数問題分類(算数の文章問題の分類)、および体(数学の世界)との対応をとってみましょう。
前回の足し算・引き算と、今回の掛け算・割り算をまとめて表します。
| 算数問題分類 | 算数域分類 | 算数群 | 体(数学の世界) | |
|---|---|---|---|---|
| 足し算 | 合併 | 集合 (時間なし) |
P @ A = S (可換) |
P + A = S (可換) |
| 増加(時間あり) | ||||
| 求大 | 求大 | F # D = M (非可換) |
F + D = M (可換) |
|
| 引き算 | 求残(時間あり) | 分離 (時間なし) |
S !@ P = A S !@ A = P |
S – P = A S – A = P |
| 求部分 | ||||
| 求差 | 求差 | M !#o F = D | M – F = D | |
| 求小 | 求小 | M !#s D = F | M – D = F | |
| 算数問題分類 | 算数域分類 | 算数群 | 体(数学の世界) | |
| 掛け算 | 長方形の求積 | 求積 | S * O = P (可換) |
S × O = P (可換) |
| 同数累加 | 求倍果 | B & T = R (非可換) |
B × T = R (可換) |
|
| 倍概念 | ||||
| 割り算 | – | 求項 | P !* O = S P !* S = O |
P ÷ O = S P ÷ S = O |
| 包含除 | 求倍数 | R !&o B = T | R ÷ B = T | |
| 倍を求める | ||||
| 等分除 | 求基数 | R !&s T = B | R ÷ T = B | |
| もとにする数を求める |
(「求項」にあたる算数問題分類は書いていませんが、長方形の面積と一辺の長さから、もう一辺の長さを求める問題はあることでしょう。)
真ん中の2つの列は、本稿で定義した世界です。
独自定義した「算数群」ですが、ここの演算子@と#をいっしょくたに「+」と書き、及び演算子*と&をいっしょくたに「×」と書くとすると、これがそのまま「順序ある派」の「しき」にあたる、ということがわかります。(「順序ない派」が、「しき」=「体」であることは、言うまでもありません。)
算数域分類と算数群は、分類がMECEかつ演算子が一意でスッキリしています。
逆に「算数問題分類」と(順序ある派の)「しき」では、分類がMECEでなく、かつ演算子が多義でConfusingですね。
(求大、求小、求差は、算数問題分類と算数域分類両方に使っておりConfusingかもしれませんが、意味と範囲が同じなので、まあ良しとします。)
まとめ
四則演算での算数群と算数域分類を定義し、算数問題分類と体との対応を取りました。
足し算や掛け算に順序があるとする場合にスッキリしない点が、順序があるかないか判別する分類がMECEでない、「しき」にした場合に演算子が多義になる、という2点であろうことが推測できました。
独自定義の「算数群」では、子供はもちろん大人も「なにそれ?」ですので、次回は子供よりの「かた」を考えてみます。

